Magnetic permeability—the cornerstone of electromagnetic material science—defines how substances respond to magnetic fields. From Maxwell’s equations to modern power systems, this fundamental property shapes technological progress. At Osencmag, we combine rigorous research with industrial expertise to advance permeability measurement and material innovation.
What is magnetic permeability?
Magnetic permeability—a material’s ability to develop an internal magnetic field under an external influence—is a cornerstone of magnetics. Coined by Oliver Heaviside in 1885, it quantifies how readily a material responds to an applied field, shaping the resulting magnetic interactions.
When a ferrous material is drawn to a magnet, permeability dictates the strength of the induced magnetization. The higher the permeability, the more intense the material’s internal field and the stronger the attraction.
Yet permeability is not static. It varies with temperature, processing history, field strength, and environmental factors—making it a dynamic property rather than a fixed value. This complexity is what makes it so compelling: permeability reveals how materials adapt to magnetic fields, offering insights into their fundamental behavior.
To study it is to explore the nuanced relationship between matter and magnetism—a field where theory and real-world response intertwine.
How to calculate magnetic permeability?
Magnetic permeability μ (Greek mu) is defined as: μ=B/H
where B is the magnetic flux density and H is the magnetic field strength.
In these systems, the permeability B/H is called the absolute permeability μ of the medium. The relative permeability μᵣ is then defined as the ratio μ / μ₀, which is dimensionless. This relationship lies at the heart of how we quantify the magnetic response of materials and is a foundational equation in electromagnetism.
What is the vacuum magnetic permeability in natural unit?
In metre–kilogram–second (mks) and SI units, the permeability of free space (symbolized μ₀) was defined as equal to 4π × 10⁻⁷ weber per ampere-metre. However, with the redefinition of the ampere in 2019, μ₀ is no longer exactly equal to 4π × 10⁻⁷, and must be determined experimentally. That said, the deviation is extremely small: [μ₀ / (4π × 10⁻⁷)] ≈ 1.00000000055, still very close to its former value.
This constancy of the vacuum’s magnetic response reminds me that even the seeming void of space holds a quiet but measurable structure—a beautiful interplay of fundamental constants.
What is magnetic permeability of free space?
The permeability of free space, also known as the permeability of air or vacuum μ₀, is one of those constants that gets tossed around frequently in electromagnetism, and yet, it’s quite the unsung hero of the physics world. Think of it as the measure of how much “magnetic freedom” space (vacuum or air) offers to the magnetic field.
Mathematically, μ₀ is the ratio of magnetic flux density B0 to the magnetic field intensity H in a vacuum:
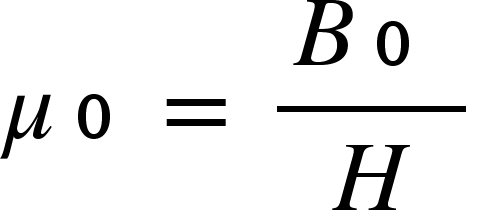
This is not just any number—it’s a physical constant that we can count on. In fact, its exact value is:
![]()
or equivalently
![]()
or in another context, μ₀ is
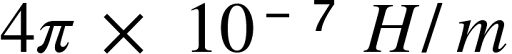
(henrys per metre)
Now, here’s the twist: μ₀ is tied to the speed of light in the most elegant way possible. There’s a beautiful equation that connects μ₀ to the speed of light c and the permittivity of free space ε0:

It’s like the perfect trio in physics—c,μ₀, and ε0—dancing together in harmony.
Now, what does this constant really do for us, practically speaking? Well, it’s used to calculate magnetic force between two electric currents. The constant μ₀ gives us a measure of how strong the magnetic force is between two wires carrying currents. Here’s the magic formula:
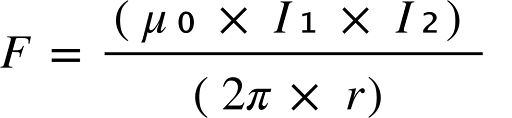
Where:
- F is the magnetic force,
- I₁ and I₂ are the currents,
- r is the distance between the wires.
Here’s a fun bit—when you define the ampere as the unit of electric current, it turns out that if each current is 1 ampere and the distance between the wires is 1 meter in a vacuum, the force per unit length between the wires is exactly:
μ₀ / 2π newtons per meter
So, in essence, the permeability of free space is not just a constant—it’s a fundamental cornerstone in understanding the magnetic forces that shape our universe.
In other words,μ₀ is like the backstage pass for electromagnetism, quietly ensuring that everything runs smoothly backstage while all the action happens on stage.
What is Absolute Permeability in Magnetism?
Absolute magnetic permeability (μ) is a measure of a material’s magnetic conductivity, or in simpler terms, how easily it lets magnetic flux pass through. The higher the permeability, the more “magnet-friendly” the material is. Think of it like the material’s “magnetic VIP pass”—if it has a high permeability, it’s got access to the magnetic flow with ease.
Now, the formula to calculate absolute permeability looks like this:
μ = μ₀ μᵣ [H/m]
Where:
- μ₀ is the absolute permeability of air or vacuum, equal to 4π × 10⁻⁷ H/m—yes, vacuum is not exactly a party for magnetic flux, but it’s got the baseline value,
- μᵣ is the relative permeability of the material (unitless), which tells us how much more magnetically “open” the material is compared to the vacuum.
To tie it all together, the relationship between magnetic flux density (B) and magnetic field strength (H) in a material is:
B = μ H = μᵣ μ₀ H
In a vacuum, things are simpler:
B = μ₀ H
Example: Imagine a material that’s 1000 times more magnetic than vacuum. Its absolute permeability would be:
μ = 1000 · μ₀ = 1000 · 4π × 10⁻⁷ ≈ 0.001257 H/m
For most non-magnetic materials, their permeability is about the same as vacuum—so their absolute permeability ends up being:
μ ≈ μ₀ = 4π × 10⁻⁷ H/m
So, in short, absolute permeability is like the “magnetic bandwidth” of a material, showing how much it allows magnetic fields to flow through. It’s a key concept when exploring how different materials behave under magnetic influence—whether they’re a magnetic powerhouse or a magnetic wallflower!
Magnetic Permeability of Various Materials.
Magnetic materials exhibit some of the most intriguing phenomena in condensed matter physics, with behaviors spanning quantum mechanical origins to macroscopic engineering applications. As both a scientist and an admirer of their elegance, I present this systematic classification while maintaining proper technical rigor.
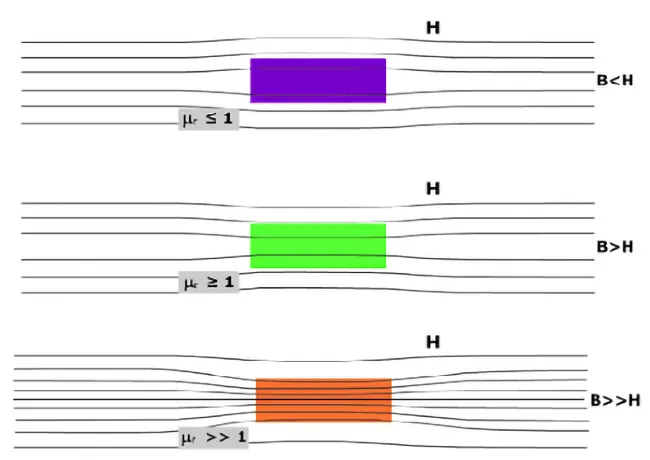
1. Diamagnetic Materials (μᵣ < 1)
Diamagnets demonstrate a fundamental quantum mechanical response—Larmor precession of electron orbitals—inducing a weak, negative magnetization opposing applied fields (χ ≈ -10⁻⁵). Their permeability (μᵣ = 1 + χ) is thus slightly below unity. While bismuth (χ = -1.66×10⁻⁴) exhibits the strongest intrinsic diamagnetism among elemental solids, superconductors represent the extreme case with perfect diamagnetism (χ = -1) via the Meissner effect.
2. Paramagnetic Materials (μᵣ > 1)
Paramagnets follow Curie’s law (χ = C/T) or Pauli paramagnetism in metals, with μᵣ ≈ 1 + 10⁻⁵ to 10⁻³. Their weak positive susceptibility arises from unpaired electron spins partially aligning with the field (H), though thermal disorder (kT) dominates at room temperature. Platinum’s paramagnetism (χ = +2.9×10⁻⁴) makes it useful in cryogenic thermometry, while rare-earth ions exhibit stronger effects due to f-electron contributions.
3. Ferromagnetic Materials (μᵣ ≫ 1, Nonlinear)
Ferromagnets defy simple permeability descriptions due to:
- Spontaneous magnetization below T_c (exchange interaction)
- Domain structure minimizing magnetostatic energy
- Hysteresis with μᵣ dependent on H-field history
Iron’s maximum μᵣ ~ 5×10⁵ (purified Fe) stems from domain wall motion and moment rotation. The Landau-Lifshitz-Gilbert equation models their dynamics, crucial for transformer cores (silicon steel, μᵣ ~ 40,000) and magnetic recording media.
4. Hard Magnetic Materials (Low μᵣ, High H_c)
Permanent magnets like Nd₂Fe₁₄B (H_c > 1 T) exhibit:
- High anisotropy energy (K₁ ~ 4.5 MJ/m³) pinning domains
- Low reversible permeability (μᵣ ~ 1.05) due to resistance to domain reorientation
- (BH)ₘₐₓ > 400 kJ/m³, enabled by microstructure engineering
Their performance derives from the Stoner-Wohlfarth model, where coercivity scales with 2K₁/Mₛ.
5. Soft Magnetic Materials (High μᵣ, Low H_c)
Soft magnetic materials—silicon steel, Ni-Fe, and Fe-Co alloys—combine high permeability (μᵣ up to 10⁵) with minimal hysteresis (H_c < 10 A/m). Their low anisotropy and domain wall mobility enable rapid magnetization reversal, making them indispensable in AC applications (transformers, motors). Key features include:
- High μᵣ: Efficient flux conduction with minimal magnetizing current
- Near-zero remanence: Reduced core losses during cyclic operation
- Engineered domain structures: Grain-oriented silicon steel (μᵣ ~ 40,000) exploits crystallographic texture to optimize performance
| Material | Relative Permeability (μ/μ₀) | Comment |
|---|---|---|
| Pure Iron (99.95%) | Up to 200,000 | High permeability; the magnetic superstar |
| Silicon Steel | 2,000 – 38,000 | Soft magnetic material, widely used in transformers |
| Nickel | 100 – 600 | Ferromagnetic, though less impressive than iron |
| Cobalt Alloys (e.g., Permalloy) | Up to 100,000 | High μ, often used in sensitive magnetic applications |
| Carbon Steel | ~100 | Modestly magnetic, often used in general structural applications |
| Ferrites | 10 – 20,000 | Ceramic-like, used at high frequencies |
| Stainless Steel (Ferritic) | 1,000 – 1,800 | Magnetic when annealed |
| Stainless Steel (Austenitic) | ~1.003 – 1.05 | Nearly non-magnetic, often considered for kitchen aesthetics |
| Aluminum | ~1.000022 | Paramagnetic, but barely so |
| Graphite | ~0.9996 | Slightly diamagnetic |
| Copper | ~0.999994 | Slightly diamagnetic and wonderfully conductive |
| Water | ~0.999992 | Diamagnetic; not magnetically exciting |
| Plastic | ~1.000 | Practically non-magnetic |
| Glass | ~1.000 | Ditto—transparent to both light and magnetism |
| Wood | ~1.00000043 | Just there—magnetically and otherwise |
FAQs
What are the units of magnetic permeability?
The units of magnetic permeability (μ) are Henries per meter (H/m) or equivalently, Newtons per ampere squared (N/A²·m). In the SI system, it’s all about making magnetic fields behave properly under electric current!
What material has the highest magnetic permeability?
The material with the highest magnetic permeability is mu-metal, an alloy of nickel, iron, and other elements. It’s so good at “concentrating” magnetic fields, it’s almost as if it’s trying to become the magnetic field itself. A real overachiever!
What is the relationship between magnetic resistivity and magnetic permeability?
Magnetic resistivity and permeability are related but not quite opposites. Magnetic permeability (μ) determines how easily a material can conduct magnetic flux, while magnetic resistivity (the inverse of magnetic conductivity) reflects how much a material resists the formation of a magnetic field. So, high permeability typically means low magnetic resistivity — a material that welcomes magnetic fields rather than resisting them.