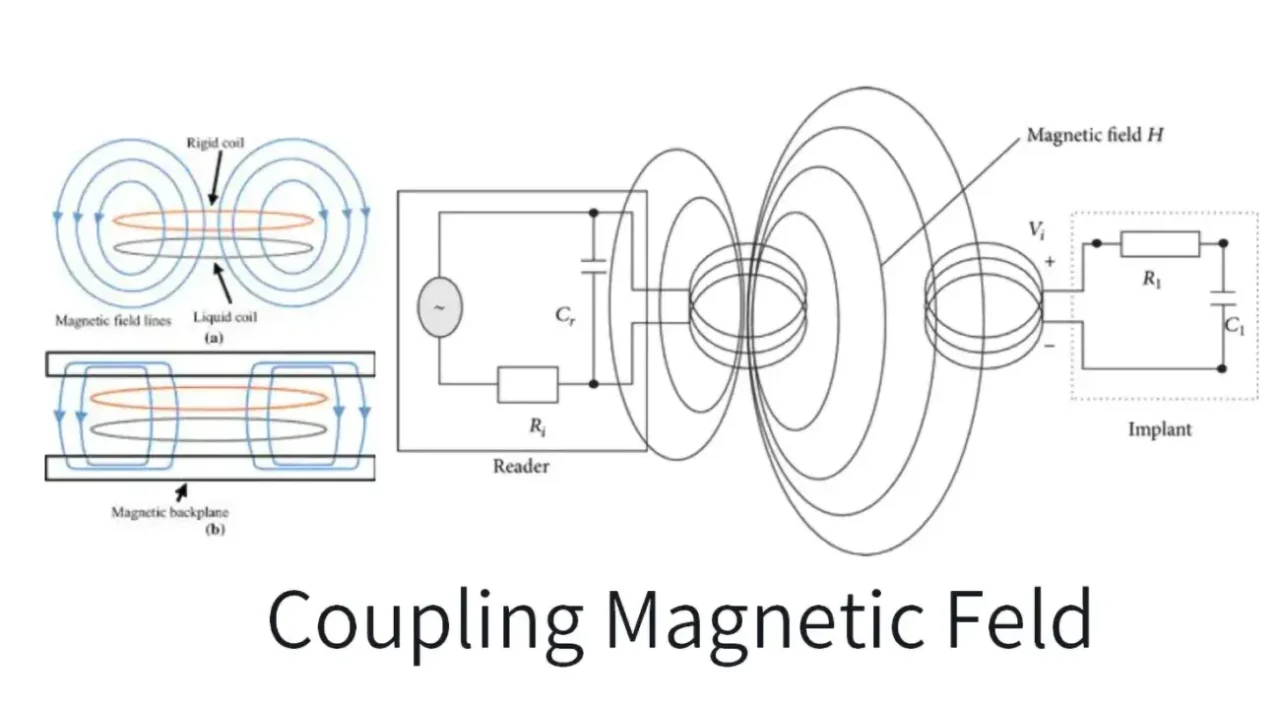
Die magnetische Permeabilität - der Eckpfeiler der elektromagnetischen Materialwissenschaft - bestimmt, wie Stoffe auf Magnetfelder reagieren. Von Maxwells Gleichungen bis hin zu modernen Energiesystemen prägt diese grundlegende Eigenschaft den technologischen Fortschritt. Bei Osencmag kombinieren wir rigorose Forschung mit industrieller Expertise, um Permeabilitätsmessungen und Materialinnovationen voranzutreiben.
Was ist die magnetische Permeabilität?
Die magnetische Permeabilität - die Fähigkeit eines Materials, unter äußerem Einfluss ein inneres Magnetfeld zu entwickeln - ist ein Eckpfeiler der Magnetik. Sie wurde 1885 von Oliver Heaviside geprägt und gibt an, wie leicht ein Material auf ein angelegtes Feld reagiert und die daraus resultierenden magnetischen Wechselwirkungen gestaltet.
Wenn ein eisenhaltiges Material von einem Magneten angezogen wird, bestimmt die Permeabilität die Stärke der induzierten Magnetisierung. Je höher die Permeabilität ist, desto intensiver ist das innere Feld des Materials und desto stärker ist die Anziehung.
Doch die Permeabilität ist nicht statisch. Sie variiert mit der Temperatur, der Verarbeitungsgeschichte, der Feldstärke und den Umgebungsfaktoren - es handelt sich also um eine dynamische Eigenschaft und nicht um einen festen Wert. Diese Komplexität macht sie so interessant: Die Permeabilität verrät, wie sich Materialien an Magnetfelder anpassen, und bietet Einblicke in ihr grundlegendes Verhalten.
Sie zu studieren bedeutet, die nuancierte Beziehung zwischen Materie und Magnetismus zu erforschen - ein Bereich, in dem Theorie und Praxis ineinandergreifen.
Wie berechnet man die magnetische Permeabilität?
Die magnetische Permeabilität μ (griechisch mu) ist definiert als: μ=B/H
wobei B die magnetische Flussdichte und H die magnetische Feldstärke ist.
In diesen Systemen wird die Permeabilität B/H als die absolute Permeabilität μ des Mediums bezeichnet. Die relative Permeabilität μᵣ ist dann definiert als das Verhältnis μ / μ₀, das dimensionslos ist. Diese Beziehung ist das Herzstück der Methode wir quantifiziert die magnetische Reaktion von Materialien und ist eine grundlegende Gleichung im Elektromagnetismus.
Wie hoch ist die magnetische Permeabilität im Vakuum in natürlicher Einheit?
In Meter-Kilogramm-Sekunden (mks) und SI-Einheiten war die Permeabilität des freien Raums (symbolisiert als μ₀) definiert als gleich 4π × 10-⁷ Weber pro Ampere-Meter. Mit der Neudefinition des Ampere im Jahr 2019 ist μ₀ jedoch nicht mehr genau gleich 4π × 10-⁷, sondern muss experimentell bestimmt werden. Allerdings ist die Abweichung äußerst gering: [μ₀ / (4π × 10-⁷)] ≈ 1,00000000055, also immer noch sehr nahe an seinem früheren Wert.
Diese Konstanz der magnetischen Reaktion des Vakuums erinnert mich daran, dass selbst die scheinbare Leere des Raums eine stille, aber messbare Struktur enthält - ein schönes Zusammenspiel von Grundkonstanten.
Was ist die magnetische Permeabilität des freien Raums?
Die Permeabilität des freien Raums, auch bekannt als Permeabilität der Luft oder des Vakuums μ₀, ist eine dieser Konstanten, die im Elektromagnetismus häufig genannt wird, und doch ist sie der unbesungene Held der Physik. Man kann sie sich als Maß dafür vorstellen, wie viel “magnetische Freiheit” der Raum (Vakuum oder Luft) dem Magnetfeld bietet.
Mathematisch gesehen ist μ₀ das Verhältnis zwischen der magnetischen Flussdichte B0 und der magnetischen Feldstärke H im Vakuum:
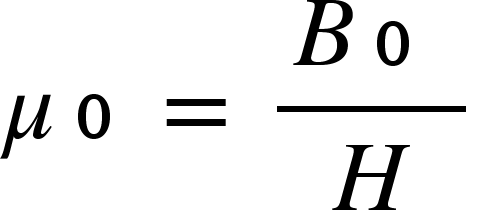
Dies ist nicht irgendeine Zahl, sondern eine physikalische Konstante, mit der wir rechnen können. Ihr genauer Wert lautet sogar:
![]()
oder gleichwertig
![]()
oder in einem anderen Zusammenhang, μ₀ ist
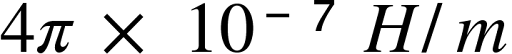
(henrys pro Meter)
Und jetzt kommt der Clou: μ₀ ist auf die eleganteste Art und Weise mit der Lichtgeschwindigkeit verknüpft. Es gibt eine schöne Gleichung, die μ₀ mit der Lichtgeschwindigkeit c und der Dielektrizitätskonstante des freien Raums ε0 verknüpft:

Es ist wie das perfekte Trio aus Physik-c, μ₀ und ε0, das gemeinsam in Harmonie tanzt.
Was bringt uns diese Konstante nun in der Praxis? Nun, sie wird verwendet, um die Magnetkraft zwischen zwei elektrischen Strömen zu berechnen. Die Konstante μ₀ gibt uns ein Maß dafür, wie stark die magnetische Kraft zwischen zwei stromführenden Drähten ist. Hier ist die Zauberformel:
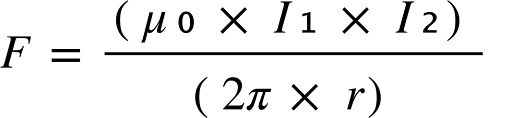
Wo:
- F ist die magnetische Kraft,
- I₁ und I₂ sind die Ströme,
- r ist der Abstand zwischen den Drähten.
Wenn man das Ampere als Einheit des elektrischen Stroms definiert, stellt sich heraus, dass bei einem Strom von 1 Ampere und einem Abstand von 1 Meter zwischen den Drähten im Vakuum die Kraft pro Längeneinheit zwischen den Drähten genau gleich ist:
μ₀ / 2π Newton pro Meter
Die Permeabilität des freien Raums ist also nicht nur eine Konstante, sondern ein grundlegender Eckpfeiler für das Verständnis der magnetischen Kräfte, die unser Universum formen.
Mit anderen Worten, μ₀ ist so etwas wie der Backstage-Pass für den Elektromagnetismus, der leise dafür sorgt, dass hinter der Bühne alles reibungslos läuft, während auf der Bühne die ganze Action stattfindet.
Was versteht man unter absoluter Permeabilität im Magnetismus?
Die absolute magnetische Permeabilität (μ) ist ein Maß für die magnetische Leitfähigkeit eines Materials, oder einfacher ausgedrückt, wie leicht es den magnetischen Fluss durchlässt. Je höher die Permeabilität, desto “magnetfreundlicher” ist das Material. Man kann sich das wie den “magnetischen VIP-Pass” des Materials vorstellen - wenn es eine hohe Permeabilität hat, hat es leichten Zugang zum magnetischen Fluss.
Die Formel zur Berechnung der absoluten Permeabilität sieht wie folgt aus:
μ = μ₀ μᵣ [H/m]
Wo:
- μ₀ ist die absolute Permeabilität der Luft oder des Vakuums, gleich 4π × 10-⁷ H/m - ja, das Vakuum ist nicht gerade ein Fest für den magnetischen Fluss, aber es hat den Basiswert,
- μᵣ ist die relative Permeabilität des Materials (ohne Einheit), die angibt, um wie viel magnetisch “offener” das Material im Vergleich zum Vakuum ist.
Um das Ganze zu vervollständigen, wird die Beziehung zwischen magnetische Flussdichte (B) und magnetische Feldstärke (H) in einem Material ist:
B = μ H = μᵣ μ₀ H
In einem Vakuum sind die Dinge einfacher:
B = μ₀ H
Beispiel: Stellen Sie sich ein Material vor, das 1000-mal stärker magnetisch ist als das Vakuum. Seine absolute Permeabilität wäre dann:
μ = 1000 - μ₀ = 1000 - 4π × 10-⁷ ≈ 0,001257 H/m
Bei den meisten nichtmagnetischen Materialien ist die Permeabilität etwa gleich groß wie das Vakuum - die absolute Permeabilität ist also gleich:
μ ≈ μ₀ = 4π × 10-⁷ H/m
Kurz gesagt, die absolute Permeabilität ist so etwas wie die “magnetische Bandbreite” eines Materials, die angibt, wie stark es magnetische Felder durchlässt. Sie ist ein Schlüsselkonzept, wenn man untersucht, wie sich verschiedene Materialien unter magnetischem Einfluss verhalten - ob sie nun ein magnetisches Kraftpaket oder ein magnetisches Mauerblümchen sind!
Magnetische Permeabilität von verschiedenen Materialien.
Magnetische Materialien weisen einige der faszinierendsten Phänomene der Physik der kondensierten Materie auf, mit Verhaltensweisen, die von quantenmechanischen Ursprüngen bis zu makroskopischen technischen Anwendungen reichen. Als Wissenschaftler und Bewunderer ihrer Eleganz stelle ich diese systematische Klassifizierung vor, ohne dabei die technische Strenge zu vernachlässigen.
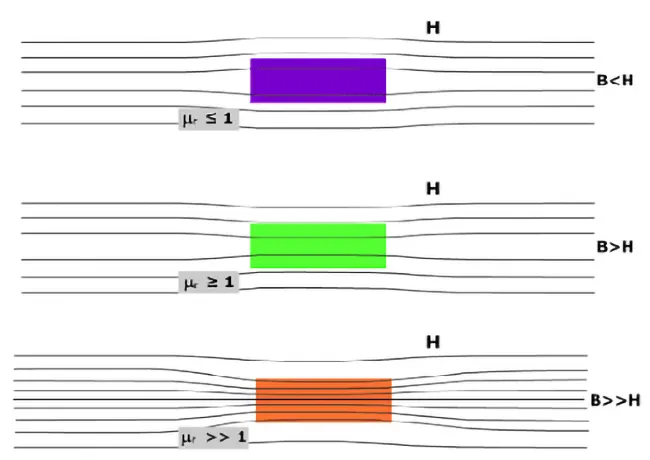
1. Diamagnetische Materialien (μᵣ < 1)
Diamagnete zeigen eine fundamentale quantenmechanische Reaktion - die Larmor-Präzession der Elektronenorbitale -, die eine schwache, negative Magnetisierung gegenüber angelegten Feldern hervorruft (χ ≈ -10-⁵). Ihre Permeabilität (μᵣ = 1 + χ) liegt daher etwas unter der Einheit. Während Wismut (χ = -1,66×10-⁴) den stärksten intrinsischen Diamagnetismus unter den elementaren Festkörpern aufweist, stellen Supraleiter den Extremfall mit perfektem Diamagnetismus (χ = -1) über den Meissner-Effekt dar.
2. Paramagnetische Materialien (μᵣ > 1)
Paramagnete folgen dem Curie'schen Gesetz (χ = C/T) oder dem Pauli-Paramagnetismus in Metallen, mit μᵣ ≈ 1 + 10-⁵ bis 10-³. Ihre schwache positive Suszeptibilität rührt von ungepaarten Elektronenspins her, die sich teilweise mit dem Feld (H) ausrichten, obwohl bei Raumtemperatur die thermische Unordnung (kT) dominiert. Der Paramagnetismus von Platin (χ = +2,9×10-⁴) macht es für die kryogene Thermometrie nützlich, während Seltenerd-Ionen aufgrund der Beiträge von f-Elektronen stärkere Effekte aufweisen.
3. Ferromagnetische Materialien (μᵣ ≫ 1, nichtlinear)
Ferromagnete widersetzen sich einfachen Permeabilitätsbeschreibungen, weil sie:
- Spontane Magnetisierung unter T_c (Austauschwechselwirkung)
- Domänenstruktur zur Minimierung der magnetostatischen Energie
- Hysterese mit μᵣ abhängig von der H-Feld-Geschichte
Das maximale μᵣ ~ 5×10⁵ (gereinigtes Fe) von Eisen ist auf die Bewegung der Domänenwand und die Drehung des Moments zurückzuführen. Die Landau-Lifshitz-Gilbert-Gleichung modelliert deren Dynamik, die für Transformatorkerne (Siliziumstahl, μᵣ ~ 40.000) und magnetische Aufzeichnungsmedien entscheidend ist.
4. Hartmagnetische Werkstoffe (niedrig μᵣ, hoch H_c)
Dauermagnete wie Nd₂Fe₁₄B (H_c > 1 T) weisen auf:
- Hohe Anisotropie-Energie (K₁ ~ 4,5 MJ/m³) in Pinning-Domänen
- Geringe reversible Permeabilität (μᵣ ~ 1,05) aufgrund des Widerstands gegen die Umorientierung der Domänen
- (BH)ₘₐₓ > 400 kJ/m³, ermöglicht durch Mikrostrukturtechnik
Ihre Leistungsfähigkeit ergibt sich aus dem Stoner-Wohlfarth-Modell, bei dem die Koerzitivfeldstärke mit 2K₁/Mₛ skaliert.
5. Weichmagnetische Materialien (hoch μᵣ, niedrig H_c)
Weichmagnetische Werkstoffe - Siliziumstahl, Ni-Fe- und Fe-Co-Legierungen - vereinen hohe Permeabilität (μᵣ bis zu 10⁵) mit minimaler Hysterese (H_c < 10 A/m). Ihre geringe Anisotropie und Domänenwandmobilität ermöglichen eine schnelle Magnetisierungsumkehr, was sie für Wechselstromanwendungen (Transformatoren, Motoren) unverzichtbar macht. Die wichtigsten Merkmale sind:
- Hohe μᵣ: Effiziente Flussleitung mit minimalem Magnetisierungsstrom
- Remanenz nahe Null: Geringere Kernverluste bei zyklischem Betrieb
- Konstruierte Domänenstrukturen: Kornorientierter Siliziumstahl (μᵣ ~ 40.000) nutzt die kristallografische Textur zur Leistungsoptimierung
| Material | Relative Durchlässigkeit (μ/μ₀) | Kommentar |
|---|---|---|
| Reines Eisen (99,95%) | Bis zu 200.000 | Hohe Permeabilität; der magnetische Superstar |
| Siliziumstahl | 2,000 - 38,000 | Weichmagnetisches Material, das häufig in Transformatoren verwendet wird |
| Nickel | 100 - 600 | Ferromagnetisch, wenn auch weniger eindrucksvoll als Eisen |
| Kobalt-Legierungen (z. B. Permalloy) | Bis zu 100.000 | Hoher μ-Wert, oft in empfindlichen magnetischen Anwendungen verwendet |
| Kohlenstoffstahl | ~100 | Geringfügig magnetisch, häufig für allgemeine strukturelle Anwendungen verwendet |
| Ferrite | 10 - 20,000 | keramikähnlich, wird bei hohen Frequenzen verwendet |
| Rostfreier Stahl (ferritisch) | 1,000 - 1,800 | Magnetisch im geglühten Zustand |
| Rostfreier Stahl (austenitisch) | ~1.003 - 1.05 | Nahezu unmagnetisch, oft für die Küchenästhetik in Betracht gezogen |
| Aluminium | ~1.000022 | Paramagnetisch, aber nur knapp |
| Graphit | ~0.9996 | Schwach diamagnetisch |
| Kupfer | ~0.999994 | Geringfügig diamagnetisch und wunderbar leitfähig |
| Wasser | ~0.999992 | Diamagnetisch; nicht magnetisch anregend |
| Kunststoff | ~1.000 | Praktisch unmagnetisch |
| Glas | ~1.000 | Ditto-transparent sowohl für Licht als auch für Magnetismus |
| Holz | ~1.00000043 | Einfach da - magnetisch und anders |
FAQs
Was sind die Einheiten der magnetischen Permeabilität?
Die Einheiten der magnetischen Permeabilität (μ) sind Henries pro Meter (H/m) oder äquivalent dazu Newton pro Ampere zum Quadrat (N/A²-m). Im SI-System geht es darum, dass sich Magnetfelder unter elektrischem Strom richtig verhalten!
Welches Material hat die höchste magnetische Permeabilität?
Das Material mit der höchsten magnetischen Permeabilität ist Mu-Metall, eine Legierung aus Nickel, Eisen und anderen Elementen. Es ist so gut darin, Magnetfelder zu “konzentrieren”, dass es fast so aussieht, als würde es versuchen, selbst zum Magnetfeld zu werden. Ein echter Überflieger!
Welcher Zusammenhang besteht zwischen dem magnetischen Widerstand und der magnetischen Permeabilität?
Der magnetische Widerstand und die Permeabilität sind miteinander verwandt, aber nicht völlig gegensätzlich. Die magnetische Permeabilität (μ) gibt an, wie leicht ein Material den magnetischen Fluss leiten kann, während der magnetische Widerstand (der Kehrwert der magnetischen Leitfähigkeit) angibt, wie sehr ein Material der Entstehung eines Magnetfelds widersteht. Eine hohe Permeabilität bedeutet also in der Regel einen niedrigen magnetischen Widerstand - ein Material, das Magnetfelder eher begrüßt als ihnen zu widerstehen.